Surveys and questionnaires often contain “scale” questions, in which the respondent is invited to rate something or to express agreement or disagreement with some proposition by choosing one of some finite number of alternatives that are presented as labelled positions along a linear scale. Such questions do not refer to any quantity that can be measured in multiples of a standard unit, but rely instead on the respondents' intuitions about the meanings of the labels.
The proponent of a scale question, in processing and interpreting the responses, frequently commits a fallacy that invalidates the reported results. Adding together the labels for the responses to a scale question, as one does (for instance) when calculating an arithmetic mean, is a nonsensical and invalid operation. Addition presupposes that the addends have a common unit. Since responses to a scale question are not multiples of a common unit, it makes no sense to add them. The operation is invalid even if the respondents' intuitions about the labels happen to agree exactly.
To see the kind of error that this fallacy produces, consider the following instance. Respondents are asked to rate something — perhaps the quality of students' work in a course. Let's represent the range of possible amounts or degrees of whatever is being rated as a line segment:
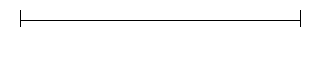
For the sake of argument, let's assume that equal distances along this line represent equal differences in whatever is being rated.
Consider two respondents, A and B, who will be asked for their assessments of two different things, X and Y. Let's suppose that their assessments of X and Y, in terms of whatever is to be rated, are as follows:
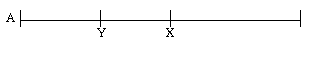

When the assessments provided by A and B are combined, with equal weight, the correct result in each case is the midpoint of the segment bounded by the two respondents' assessments:
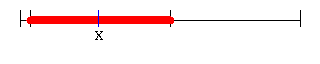
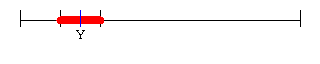
Since the mean for X is higher than the mean for Y, the collective assessment of the respondents is that X has a larger amount or a higher degree of whatever is being rated than Y.
Suppose now that the respondents are asked to report their assessments on a scale with six labels, using 1 as the label for the lowest rating and 6 for the highest. We'll assume, again for the sake of argument, that the respondents' intuitions about the meanings of the six labels agree, and that the correspondence between labels and positions on our line segment is as follows:
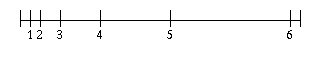
This might well be the case if the respondents are, for instance, professors at an institution where grade inflation is a problem.
Using this scale, respondent A gives X a rating of 5 and Y a rating of 4, while respondent B gives X a rating of 1 and Y a rating of 3. The sum of X's ratings is 6 and their mean is 3; the sum of Y's ratings is 7 and their mean is 3.5. So, going by the ratings, one would incorrectly conclude that the respondents together rated Y more highly than X.
The fallacy is now obvious: Y's ratings are inflated. The supposed units that make up the supposed quantity “4 + 3” correspond to smaller amounts or lesser degrees of whatever is being rated than the supposed units that make up X's “5 + 1.” The operations of adding and averaging the ratings conceal this inflation because they incorrectly presuppose that the numerical labels are multiples of a fixed unit.
Adding and averaging are, if possible, even more nonsensical when respondents' intuitions about the significance of the various labels differ.
When what is being rated is not a quantity at all, it is not appropriate to represent it by any kind of linear scale in the first place. In such cases (which are nevertheless extremely common), the use of a scale question is not merely fallacious, but just silly.